Introduction to Computing
There are 3 kind of number systems.
- Base 10 (Decimal)- Human beings use. These are 0,1,2,3,...9
- Base 2 (Binary)- Computer use binary numbers. These are only 0 and 1, and these digits are commonly referred to as bits.
- Base 16 (Hexadecimal)-hexadecimal system,is used as a convenient representation of binary numbers.
- The ASCII (pronounced “ask-E”) code assigns binary patterns for
- Numbers 0 to 9
- All the letters of English alphabet,uppercase and lowercase
- Many control codes and punctuation marks
- The ASCII system uses 7 bits to represent each code
Conversion System:
Decimal to Binary conversiton
- Divide the decimal number by 2 repeatedly
- Keep track of the remainders
- Continue this process until the quotient becomes zero
- Write the remainders in reverse order to obtain the binary number
Binary to Decimal Conversion:
- Know the weight of each bit in a binary number
- Add them together to get its decimal equivalent
Decimal to Binary conversiton Through Weights
- Use the concept of weight to convert a decimal number to a binary directly
Represent a Binary in Hexadecimal Number
- Start from the right and group 4 bits at a time, replacing each 4-bit binary number with its hex equivalent
From Hex to Binary Conversion
- Each hex digit is replaced with its 4-bit binary equivalent
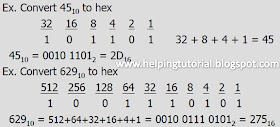
Decimal to Hex Conversion
There are two methods to achieve this task.
- Convert to binary first and then convert to hex
- Convert directly from decimal to hex by repeated division, keeping track of the remainders
Hex to Decimal Conversion
There are Two Methods to achieve this.
- Convert from hex to binary and then to decimal
- Convert directly from hex to decimal by summing the weight of all digits
Addition of two digits
- Adding the digits together from the least significant digits
- If the result is less than 16, write that digit as the sum for that position
- If it is greater than 16, subtract 16 from it to get the digit and carry 1 to the next digit
Subtraction
- If the second digit is greater than the first, borrow 16 from the preceding digit









No comments:
Post a Comment